triosql.blogg.se - Raise amount of bins of histogram in excel 2016

#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 FOR MAC#
#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 INSTALL#
#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 UPDATE#
#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 MANUAL#
#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 DOWNLOAD#

Activating “Analysis Tool Pack” in Excel Macįollow these simple steps to activate “Analysis Tool Pack” in Excel Mac

#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 DOWNLOAD#

…make sure to download this sample file to follow along.

#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 INSTALL#

To create a histogram in the Mac version of Excel we need to install “Analysis Tool Pack” as well.

#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 FOR MAC#

When you create a histogram using “Analysis Took Pack” you can’t undo it, you need to delete it and create a new one if you want to make changes.Ĭreating a Histogram in the Excel for Mac.

If you skip specifying the bins, it will automatically choose bins and creates the chart.

#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 UPDATE#

When you add a new value in the main data it will not update it, so you need to create a new chart.

“Analysis Took Pack” creates a chart that is not dynamic.

Even if you don’t have a value greater than the last bin it adds “More” as a bin.

Apart from the bins you create, it adds an extra bin with the name of “More” to show values more than the last bin.

The first bin includes lower than the value from itself and the rest of the bins include the lower than values from itself and greater values from the previous bin.

Important Points You Need to Understand when you are using “Analysis Took Pack” to Create a Histogram in Excel Square root (of data size) estimator, used by Excel and other programs for its speed and simplicity.…here’s the sample file with a histogram created using “Analysis Tool Pack”. Only optimal for gaussian data and underestimates number of bins for large non-gaussian datasets. R’s default method, only accounts for data size. Commonly overestimates number of bins required. Can be regarded as a generalization of Scott’s rule.Įstimator does not take variability into account, only data size. Less robust estimator that that takes into account data variability and data size.Įstimator based on leave-one-out cross-validation estimate of the integrated squared error. Robust (resilient to outliers) estimator that takes into account data variability and data size.Īn improved version of Sturges’ estimator that works better with non-normal datasets. Maximum of the ‘sturges’ and ‘fd’ estimators. Default approach follows partially Rob Hyndman's recommendation Here is the list

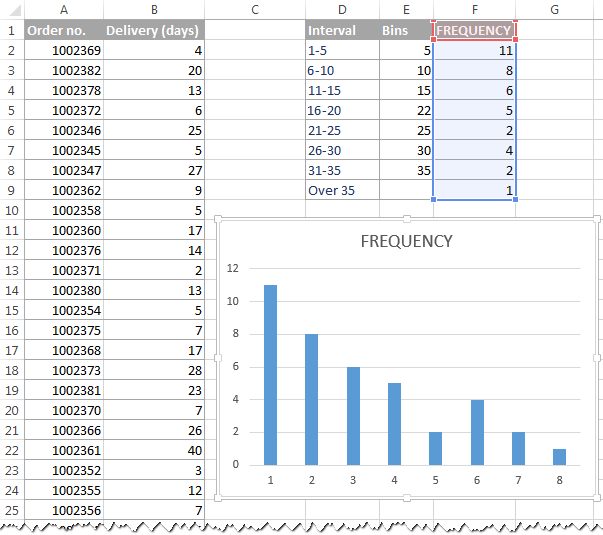
#RAISE AMOUNT OF BINS OF HISTOGRAM IN EXCEL 2016 MANUAL#

Numpy's manual page on histogram_bin_edges provides nice list and pros and cons of each approach. Then, one should find a stable/robust method that does not change with changing data. If binning changes the inference or results of the upstream task. Experience tells, this depends on the upstream task as well. With so few data, what approaches should I take to calculating the number of bins to use?įD or doane methods (see below) might be more suitable. Spike histograms are similar to rug plots, and the human eye is quite good at summarizing distributional shapes from examining tick mark density in the rug. You'll also see an example where horizontal lines are added underneath the histogram to show various quantiles as in a box blot. Many examples are shown here including interactive spike histograms where data values can be viewed in hover text. The key algorithm is here in for example the histboxp function. The result is "spike histograms" which I've implemented in many functions in the R Hmisc package. For that reason I use either m=100 or 200 bins regardless of the sample size, with modifications to (1) have unequally spaced bins when the number of distinct data values is not huge and (2) to pool such unequally spaced bins when two distinct data values are closer together than, say, 1/5m of the data span. I believe that histograms need to be both summary and descriptive measures. This clashes with the need to show individual outliers, digit preference, bimodality, data gaps, and other features. Scroll past that to see the theory and explanation, then keep scrolling to find links to the papers that explain the method.Ĭonventional wisdom dictates that a "broken look' resulting from a histogram with many bins is undesirable. It is a bit more complicated to calculate, but seems to do a great job.

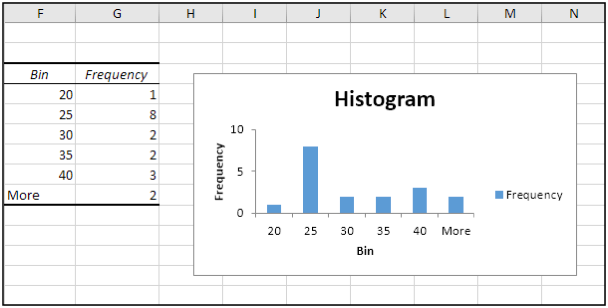
This page from Hideaki Shimazaki explains an alternative method. The simplest method is to set the number of bins equal to the square root of the number of values you are binning. This wikipedia page lists several methods for deciding bin width from the number of observations. If you have lots of values, your graph will look better and be more informative if you have lots of bins. The decision clearly depends on the number of values.

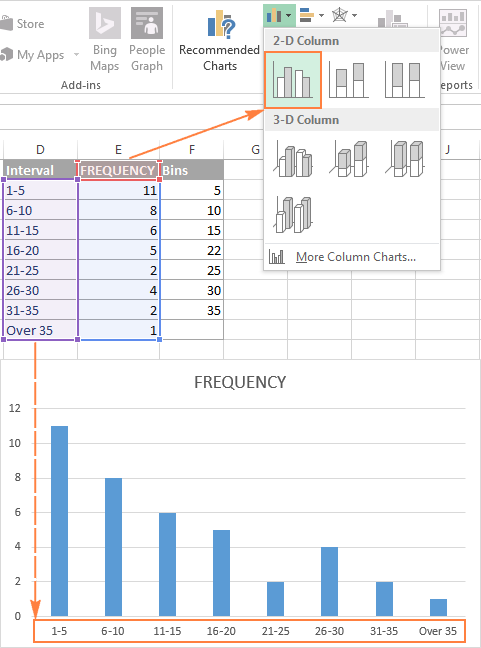
If you want to create a frequency distribution with equally spaced bins, you need to decide how many bins (or the width of each). Either a dot plot, or a cumulative frequency distribution, which doesn't require any bins. One solution is to create a graph that shows every value. If you have too many bins, you get a broken comb look, which also doesn't give a sense of the distribution. If you use too few bins, the histogram doesn't really portray the data very well.